Del problema que viene ahora lo interesante es la respuesta que se obtiene, porque contiene una explicación curiosa, una forma distinta de ver algo que seguramente ya sabéis antes de leerla.

    En geometría se estudian y se clasifican muchos tipos de transformaciones del plano. Si esto es algo conocido para vosotros podéis saltaros los dos párrafos siguientes.

    Una transformación no es más que una aplicación del plano en el plano, es decir: una regla que nos dice, dado un punto cualquiera del plano, qué otro punto le corresponde. Un ejemplo de aplicación es la que multiplica por dos las coordenadas de los puntos: si nos dan un punto (x,y), el punto que le corresponde según esta aplicación es el (2x, 2y). Se puede entender una transformación como algo que "cambia" una figura dibujada en el plano de la siguiente forma natural: si hay un dibujo hecho (que consiste, digamos, de puntos negros) le aplicamos la transformación a cada uno de los puntos negros de dicho dibujo y dibujamos puntos negros en cada uno de los lugares que obtengamos (y borramos el dibujo original). Las transformaciones afines (como todas las que se mencionan aquí) son aquéllas que siempre que transforman una línea recta dan como resultado otra línea recta. A veces se les llama lineales, un nombre del que podéis ver la razón, pero la palabra "lineales" se reserva a veces para un tipo especial de las afines.

    Por ejemplo, algunas transformaciones afines son traslaciones, que simplemente lo desplazan todo en una dirección dada una cierta distancia fija. Si hubiese algo dibujado en el plano el resultado de aplicar esta transformación sería que el dibujo se movería en esa dirección, como si moviésemos un papel sin girarlo. Otras son las semejanzas, que multiplican todas las distancias por el mismo factor. El efecto de esto es hacer una "fotocopia" ampliada o reducida de cualquier cosa que esté en el plano. El ejemplo de antes (el que llevaba (x,y) hasta (2x, 2y)) es una semejanza que multiplica todas las distancias por dos.

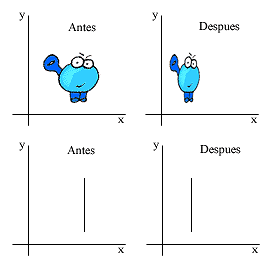
    Una compresión en una dirección dada es el equivalente a estirar o encoger una tela de goma en esa dirección: es una aplicación que reduce o aumenta las distancias a una cierta recta dada según un cierto factor. La aplicación que lleva (x,y) en ((1/2)x, y) es un ejemplo de esto. En el dibujo podemos ver el efecto que causaría esta compresión horizontal sobre un muñequillo y sobre un trozo de recta vertical. Se han dibujado unos ejes para tener una referencia.

    Observamos que el muñequillo se aplasta horizontalmente, manteniendo su altura. Además, se desplaza un poco hacia la izquierda porque lo hemos dibujado a la derecha del eje vertical (es como si estuviera a un lado de la goma cuando la encogemos). Sin embargo la recta, como no puede aplastarse porque tiene ancho cero, sólo se desplaza. Curiosamente, aplastar una recta en una dirección perpendicular a la suya no hace más que trasladarla; la recta sigue siendo igual. Lo mismo ocurre con una recta completa (infinita) si la aplastamos en su misma dirección: ésta se queda exactamente igual. ¿Pasará esto con alguna cosa que no sean rectas o trozos de recta?.

    ¿Existe alguna otra figura que no esté formada por rectas y que al comprimirla horizontalmente dé como resultado la misma figura (tal vez desplazada)?

Aclaración: hay respuestas triviales a esta pregunta, como todo el plano, o un conjunto de puntos alineados verticalmente... ¡Pero hay también una figura muy interesante que cumple esto y no es trivial en absoluto!

Nota [08/09/2003]: Planteada así, la pregunta era demasiado ambigua. En un mensaje, Manolo Sánchez me dice que hay muchas figuras que cumplen lo que se pide, y que además todas se obtienen partiendo de un dibujo cualquiera, el que uno elija, y añadiéndole todas las figuras que resultan de comprimir el dibujo a la mitad en una dirección, más todas las que resultan de ampliarlo al doble en la misma dirección. En sus palabras,

    "De este último caso, es fácil construir infinitos ejemplos no triviales. Llamemos t(A) al transformado del objeto A que se obtiene estirando horizontalmente con razón 1:2. Consideremos la unión de los objetos A, t(A), t ²;(A), t ³(A), etc. y t ^-1(A), t ^-2(A), etc. Este objeto verifica la propiedad pedida. Si el objeto inicial es, por ejemplo una circunferencia, el objeto de anchura infinita final no está formado por rectas ni segmentos."

    Así que quiero añadir algo a la pregunta:

    ¿Es posible encontrar una figura como la que se pedía que esté formada por una sóla línea curva (posiblemente infinita)?

    Con más precisión, ¿existe una figura como la que se pedía que sea homeomorfa a una línea recta infinita (a la recta real)?

    Os prometo que la respuesta es curiosa. Verdaderamente, una figura interesante.